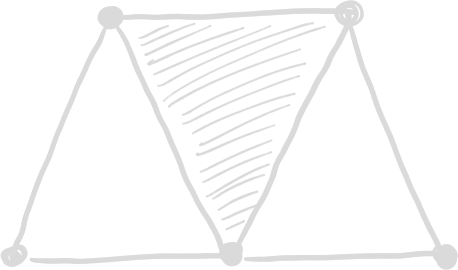
Homologie persistante
SMACUD1L - Master IMD
Observations :
- Le nombre de trous varie en fonction du paramètre
- Certains trous restent dans les étapes suivantes
- Si on bouge un peu les points, le comportement global est similaire
Rappel d'homologie
- \(K\) : complexe simplicial fini
- \(K_q\) : simplexes de \(K\) de dimension \(q\)
- \( (C, \partial) \) : complexe de chaînes induit par \(K\) avec anneau de coefficients = \(\mathbb{Z}/2\mathbb{Z} \) (corps)
- \(H_q = \ker(\partial_q) / \text{im}(\partial_{q+1}) \) : groupe d'homologie de dimension \(q\) de \(K\) (espace vectoriel)
- \(\beta_q = \dim(H_q)\) = nombre de Betti de dimension \(q\)
Exemple 1
Cycles, classes d'équivalence, base d'homologie :


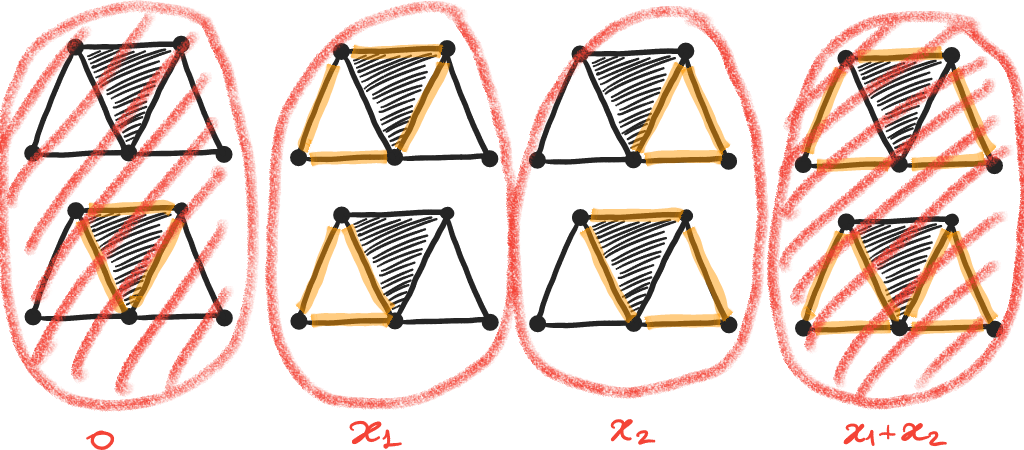
Soient \(K \subset K'\). L'application inclusion \(inc : K \longrightarrow K'\) induit une application linéaire \[\iota : H_q(K) \longrightarrow H_q(K')\] entre ses groupes d'homologie (exercice)
Exemple 2
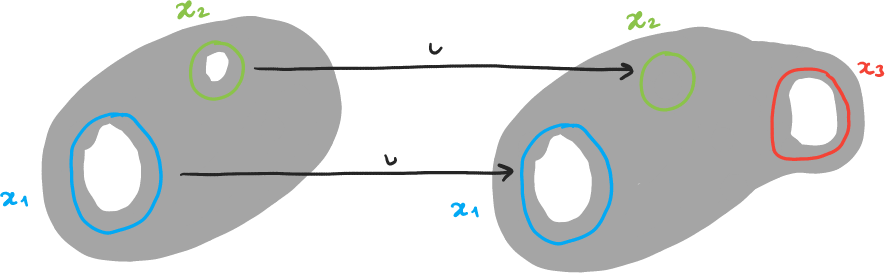
Même nombre de trous, mais
- \(\iota\) n'est pas injective ⇒ « un trou de K est bouché dans K' »
- \(\iota\) n'est pas surjective ⇒ « K' a un trou qui n'était pas dans K »
Définir la persistante
Filtration : suite de complexes imbriqués \[K^1 \subset K^2 \subset \cdots \subset K^n\]

Exemple 3
Soit \(f: K \rightarrow \mathbb{R}\) telle que :
- \(\sigma \subset \tau \Rightarrow f(\sigma) \leq f(\tau)\)
- \( f(K) = \{a_1 < a_2 < \cdots < a_n\} \)
Alors \( f^{-1}(-\infty, a_1] \subset f^{-1}(-\infty, a_2] \subset \cdots \) est une filtration (exercice)
Exercice 1
Compléter cette fonction pour qu'elle définisse une filtration
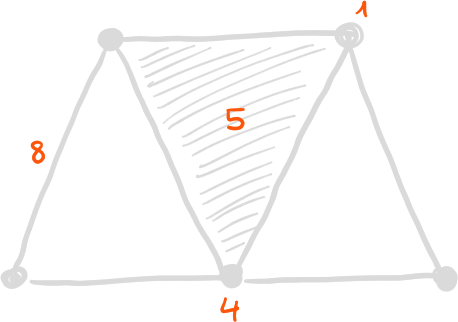
Exemple 4
Soit \(f: K_0 \rightarrow \mathbb{R}\) quelconque. On définit \( \bar{f}: K \rightarrow \mathbb{R} \)
- \( \bar{f}(\sigma) = f(\sigma) \), si \( \sigma \in K_0 \)
- \( \bar{f}(\sigma) = \max\{f(\tau) \vert \tau \subset \sigma, \tau \in K_0\} \), sinon
Alors \( \bar{f} \) définit une filtration (exercice)
Exercice 2
Éteindre cette fonction aux simplexes de dimension supérieure
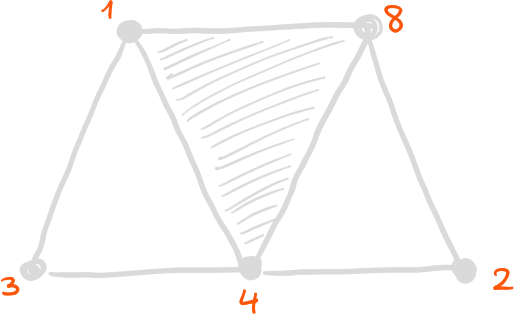
Exemple 5
Soit \(K^1 \subset \cdots \subset K^n\) une filtration. On définit \( f: K^n \rightarrow \mathbb{R} \), \( f(\sigma) = i \Leftrightarrow \sigma \in K_{i} \setminus K_{i-1} \)
Alors \( f \) définit la filtration donnée (exercice)
Donc, on peut travailler avec une filtration (suite de complexes) ou avec une fonction monotone : \( \sigma \subset \tau \Rightarrow f(\sigma) \leq f(\tau) \)
Soit \( f \) monotone, \( f(K) = \{ a_1, \cdots, a_n\} \). Notation :
- \( K^i = f^{-1}\left( -\infty, a_i \right] \)
- \(\iota_q^{i,j}: H_q(K^i) \longrightarrow H_q(K^j)\) application linéaire induite par l'inclusion (\( 1 \leq i \leq j \leq n \))
- \( \beta_q^{i,j} = \dim( \text{im}(\iota_q^{i,j}) ) \) : nombres de Betti persistants
- \( \mu_q^{i,j} = \beta_q^{i,j-1} - \beta_q^{i-1,j-1} - \beta_q^{i,j} + \beta_q^{i-1,j} \) (\( 1 \leq i < j \leq n+1,\quad \beta_q^{0,j} = \beta_q^{i,n+1} = 0 \))
Exercice 3
- Quelle inégalité entre \( \beta_q(K^i) \) et \( \beta_q^{i,j} \) ?
- Quelle inégalité entre \( \beta_q(K^j) \) et \( \beta_q^{i,j} \) ?
En français
- \( \beta_q^{i,j-1} \) = nombre de trous de \( K^i \) qui sont encore dans \( K^{j-1} \)
- \( \beta_q^{i,j-1} - \beta_q^{i-1,j-1} \) = nombre de trous qui apparaissent dans \( K^i \) et sont encore dans \( K^{j-1} \)
- \( \beta_q^{i,j} - \beta_q^{i-1,j} \) = nombre de trous qui apparaissent dans \( K^i \) et sont encore dans \( K^{j} \)
- \( \mu_q^{i,j} \) = nombre de trous qui apparaissent dans \( K^i \) et disparaissent dans \( K^{j} \)
Le diagramme de persistance de dimension q de \( f \) est le multi-ensemble \( D_q(f) \subset \overline{\mathbb{R}}^2 \) avec
- les points \( (a_i, a_j) \) avec multiplicité \( \mu_q^{i,j} \) (\( a_{n+1} = \infty \))
- les points \( (x, x) \) avec multiplicité \( \infty \), pour tout \( x \in \mathbb{R} \)
Les \( (a_i, a_j) \) sont les paires de persistance
Exemple 6
Homologie persistante de dimension 0
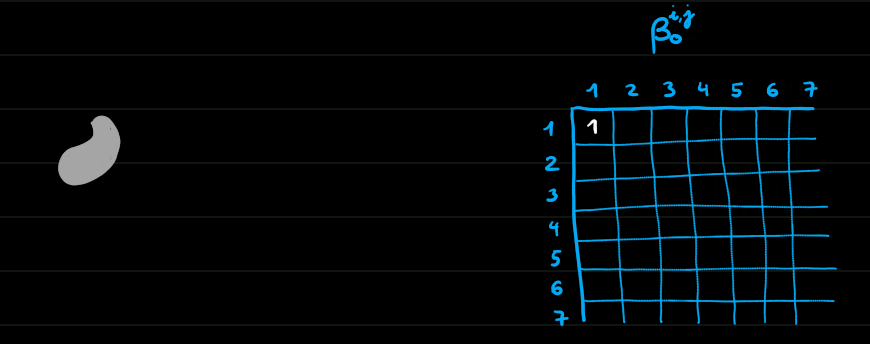
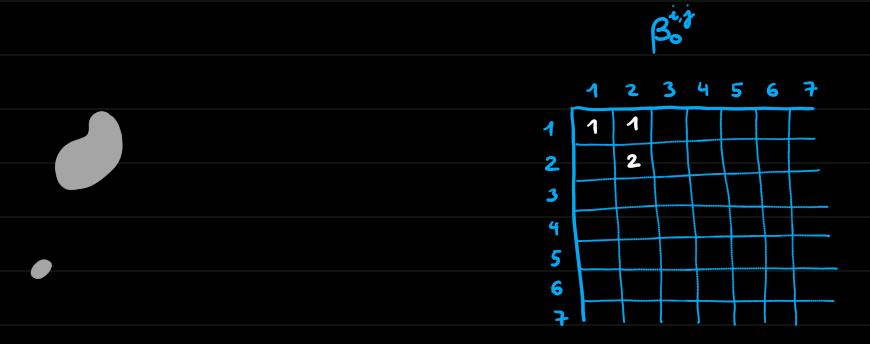
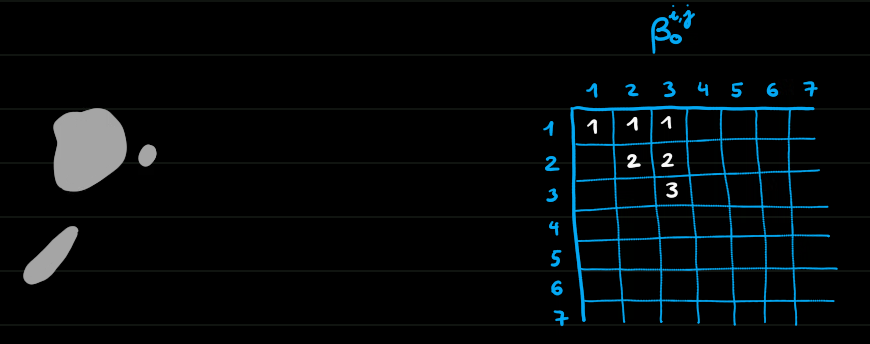
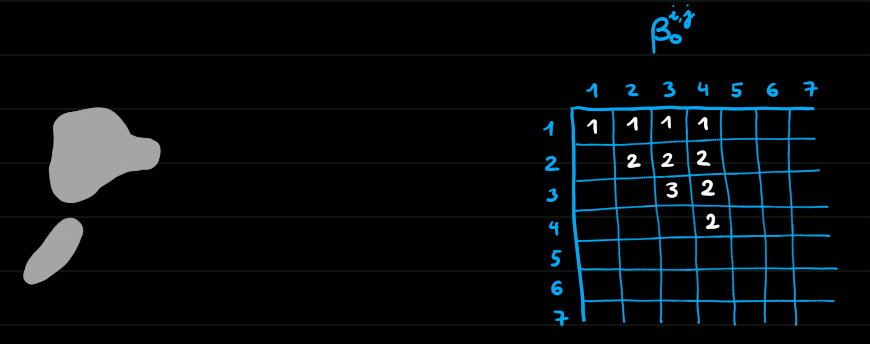
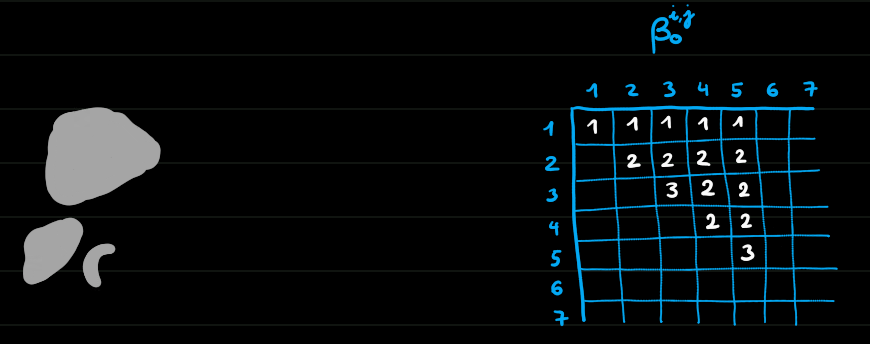
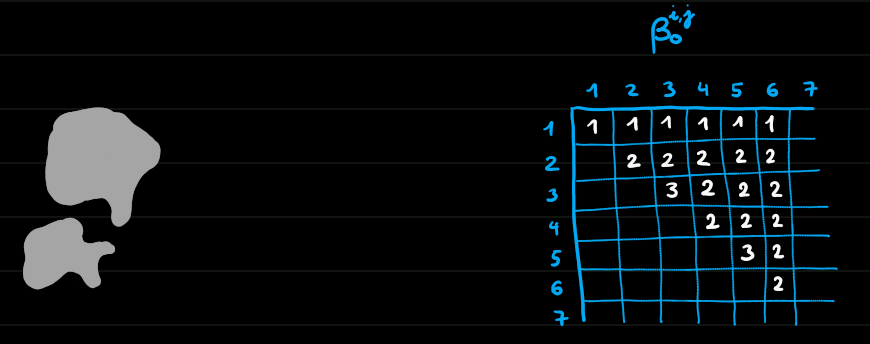
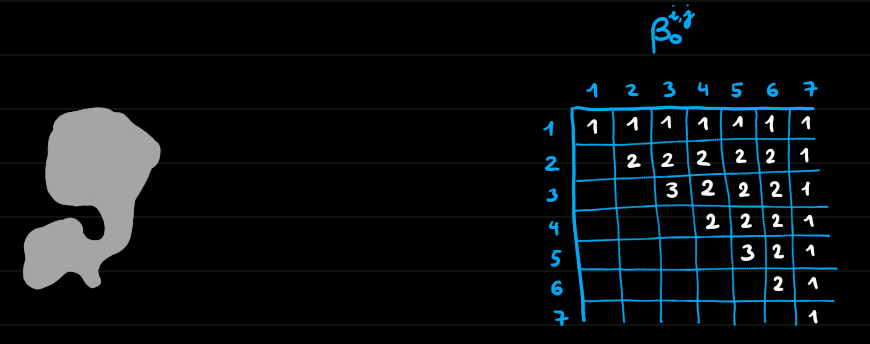

Morale
- On peut suivre les trous d'un complexe à un autre dans une filtration (ils ne sont pas indépendants)
- L'homologie persistante permet de définir la date de naissance et de mort d'un trou, donc aussi sa durée.
Stabilité
Soient \( f, g: K \longrightarrow \mathbb{R} \). Leur distance est \[ \|f-g\|_{\infty} = \max_{\sigma \in K} |f(\sigma) - g(\sigma)| \]
Question : si \( f \) et \( g \) sont similaires, que se passe-t-il avec leurs diagrammes de persistance ? Comment les comparer ?
Distance de Hausdorff
Soient \( X, Y \) deux multi-ensembles de points de \( \mathbb{R}^2 \), \[ \begin{align*} d_H(X,Y) = \max \{ &\max_{x \in X} \min_{y \in Y} \|x-y\|_{\infty},\\ &\max_{y \in Y} \min_{x \in X} \|x-y\|_{\infty} \} \end{align*} \]
- Prends un \( x \in X \), regarde sa distance vers \( Y \)
- Fais la même chose pour chaque \( x \in X \) et prends la plus grande distance
- Échange \( X \) et \( Y \), prends encore la plus grande
Exercice 4
Distance de Hausdorff ?

Premier théorème de stabilité Cohen-Steiner et al, 2007
\[ d_H(D_q(f), D_q(g)) \leq \|f-g\|_{\infty} \]
En français : si on change un peu la fonction d'une filtration, son diagramme de persistance aura ses points à coté
Exemple 7
Fonction \( f \) continue définie sur \( K \) un intervalle
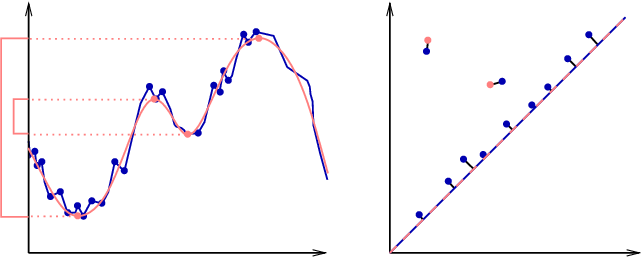
Une idée de pourquoi :
- Soit \( \delta = \|f-g\|_{\infty} \)
- \( f^{-1}(-\infty, x] \subset g^{-1}(-\infty, x + \delta] \)
- \( g^{-1}(-\infty, x] \subset f^{-1}(-\infty, x + \delta] \)
- On se sert de ces inclusions pour démontrer le théorème...
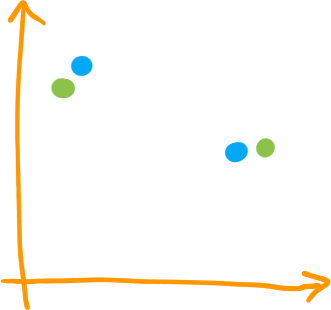
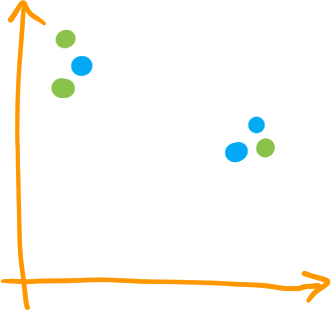
Distance bottleneck
\[ d_B(X,Y) = \min_{\gamma} \max_{x \in X} \|x - \gamma(x)\|_{\infty}, \] où \( \gamma:X \rightarrow Y \) bijective
- Fais un couplage entre les points de \( X \) et \( Y \), prends la plus grande distance entre les couples
- Parmi tous les couplages, prends la valeur la plus petite
Exercice 5
Distance bottleneck ?
Deuxième théorème de stabilité Cohen-Steiner et al, 2007
\[ d_B(D_q(f), D_q(g)) \leq \|f-g\|_{\infty} \]
En français : si on change un peu la fonction d'une filtration, chaque point va bouger d'un peu
Comme \( d_H(X,Y) \leq d_B(X,Y) \), ce deuxième théorème est meilleur
Morale
Les théorèmes de stabilité nous disent que :
- Si la fonction contient des erreurs (estimation), les diagrammes restent pareils.
- Les points près de la diagonale ( = trous avec une courte durée) ne sont pas importants (car indistinguables d'une erreur)
- Deux diagrammes différents ⇒ deux fonctions différentes, mais pas le contraire.
Exercice 6
Deux fonctions très différentes avec des diagrammes identiques ?