Morphologie mathématique
Géométrie discrète - Master GIG
Algorithmes morphologiques
Extraction de contour
Contour = supprimer l'intérieur : \[ \beta(A) = A - (A \ominus B) \]
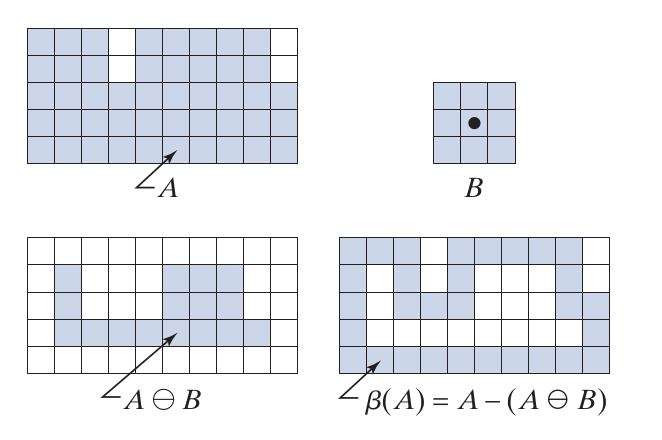
Exercice
Quel élément structurant pour le contour avec
- 4-connexité
- 8-connexité
Rappel : le contour d'un objet avec la 4-connexité sont les points de l'objet qui sont 8-adjacents de son complémentaire
Reconstruction morphologique
Reconstruire une partie de l'objet avec des dilatations et des intersections
- \( A' \subset A \) (érosion, ouverture)
- \( \delta_{B}^{A}(A') = \delta_B(A') \cap A \) : dilatation géodésique
- \( R_B^A(A') = \delta_{B}^{A} \cdots \delta_{B}^{A}(A') \) : dilatations géodésiques jusqu'à stabilité
Exemple
Filtrer les caractères hauts



Remarques :
- On récupère tous les détails de l'objet initial sauf pour les composantes connexes manquantes
- Peut être mieux que l'ouverture, qui supprime les détails fins.
Amincissement
Utiliser la transformée en tout-ou-rien pour détecter des points non-centraux et les supprimer :
- Masques : \( B^1, \ldots, B^8 \)
- \( \theta_B(A) = A - A \odot B\)
- \( X_{k+1} = \theta_{B^8} \cdots \theta_{B^1}(A) \)

Exercice
Calculer l'amincissement de cet objet :
Enveloppe convexe
Utiliser la transformée en tout-ou-rien pour détecter des points non-convexes et les ajouter : \[ X_{k+1} = X_k \cup (X_k \odot B^1) \cup \cdots \cup (X_k \odot B^{12}) \]

Remarques :
- on utilise tous les masques en même temps
- la convexité n'est pas une propriété locale : ça ne marche pas très bien
Squelette
- Problème : trouver les centres des boucles maximales.
-
Solution : faire des ouvertures et garder les résidus
\[ \sigma(A) = \cup_{k \geq 0} \left( \varepsilon_B^k(A) - \varepsilon_B^k(A) \circ B \right) \]
S ← ∅ while A not empty S ← S ∪ (A - A ∘ B) A ← A ⊖ B return S
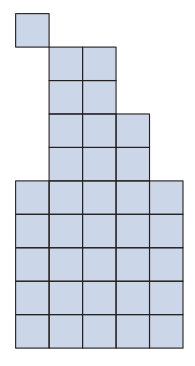
Exercice
Calculer le squelette de cet objet :
Propriétés :
- Le squelette n'est pas fin en général
- Le squelette n'est pas connexe en général
- Mais on peut reconstruire l'objet initial avec des dilatations
Élagage (pruning)
- Problème : supprimer les branches d'un squelette depuis les extrémités
- Solution : détecter les extrémités avec la transformée en tout-ou-rien
C'est un amincissement avec les masques

Exercice
Élaguer cet objet :
Squelettes
Objectif : représentation compacte d'un objet discret. Propriétés souhaitées :
- Même géométrie
- Épaisseur nulle
- Même topologie (même nombre de composantes connexes et de trous)
- Invariant aux transformations affines (squelette de la rotation = rotation du squelette)
- Inversible
- Robustesse (deux objets similaires ont des squelettes similaires)
Axe médian (continu)
- \( X \subset \mathbb{R}^2 \)
- Boule maximale : \( B(x, r) \) telle que \( B(x, r) \subset B(x', r') \subset X \Rightarrow B(x, r) = B(x', r') \)
- Une boule maximale touche la frontière de \( X \) (au moins) deux fois.
- \( S(X) \) = union des centres de toutes les boules maximales
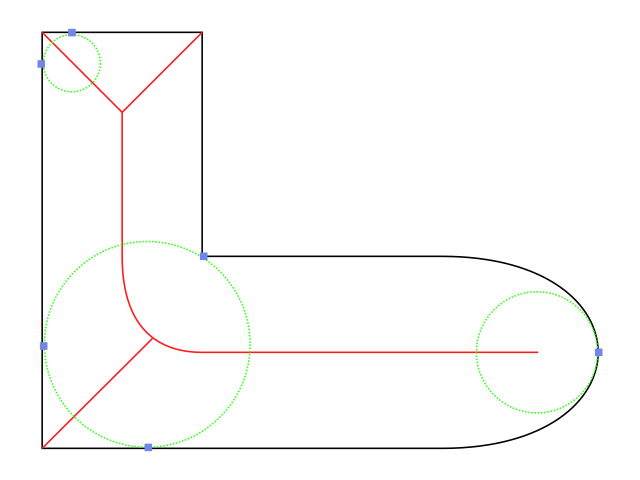
Propriétés :
- Même géométrie
- Épaisseur nulle
- Même topologie
- Invariant aux transformations affines
- Inversible (avec la transformée en distance)
Robustesse
Axe médian (discret)
Algorithme vu tout à l'heure
Propriétés :
- Même géométrie
- Épaisseur nulle (presque)
Même topologieInvariant aux transformations affines- Inversible
Robustesse
L'axe médian discrète n'a pas de bonnes propriétés, il faut chercher une approche différente.
Concentrons-nous sur la topologie
Topologie discrète
Quelques notions déjà abordées :
- 4-connexité, 8-connexité
- Composantes connexes, trous
- Équivalence d'homotopie (même topologie)
Formalisons cela avec les complexes cubiques
Complexe cubique
Éléments :
- 2-cube (carré unité) : \( [x, x+1] \times [y, y+1], (x,y) \in \mathbb{Z}^2 \)
- 1-cube (segment unité): \( [x, x+1] \times [y, y], [x, x] \times [y, y+1], (x,y) \in \mathbb{Z}^2 \)
- 0-cube (point) : \( [x,x] \times [y,y], (x,y) \in \mathbb{Z}^2 \)
Un ensemble de *-cubes est un complexe cubique s'il est fermé par inclusion : \( \sigma \subset \tau, \tau \in K \Rightarrow \sigma \in K \)
Complexe cubique d'un objet discret (avec 8-connexité) : \( K = \{ [x,x+1] \times [y,y+1] : (x,y) \in A \} \) plus leurs sous-cubes
Complexe cubique avec 4-connexité : même définition en utilisant le complémentaire.
Exemple
Complexes cubiques avec 4- et 8-connexité 
Propriétés :
- Le complexe cubique \(K\) est un sous-espace de \( \mathbb{R}^2 \), sa topologie est bien définie
- Nombre de composantes connexes de \(A\) = nombre de composantes connexes de \(K\)
- Nombre de trous de \(A\) = nombre de composantes 4-connexes finies de \(A^c\) = nombre de trous de \(K\)
Mais on savait déjà faire ça
Caractéristique d'Euler-Poincaré
- \( \chi(X) = \) nombre de composantes connexes moins nombre de trous
- Invariant topologique : deux objets avec la même topologie ont la même caractéristique d'Euler-Poincaré
- Sur un complexe cubique = \( k^0 - k^1 + k^2\), points - segments + carrés
Il est plus facile de le calculer sur le complexe cubique de l'objet discret
Exercice
Calculer la caractéristique d'Euler-Poincaré 
On peut calculer la caractéristique d'Euler-Poincaré directement sur l'objet avec la transformée en tout-ou-rien
\[ \chi(A) = |A \odot B^1| - |A \odot B^2|\]

Preuve :
- Décomposer le complexe cubique en motifs
- Trouver les configurations avec une caractéristique non nulle
- Trouver l'objet discret qui produit ce motif
Points simples
Problème : comment calculer un squelette qui a la même topologie que l'objet discret ?
Comme dans l'algorithme d'amincissement, on va supprimer des points qui ne changent pas la topologie.
Collapse élémentaire Suppression dans un complexe cubique \( K \) d'une paire de cubes \( (\sigma, \tau) \) tels que :
- \( \sigma \subset \tau \)
- Les deux cubes sont de dimensions consécutives (0–1 ou 1–2)
- \( \sigma \) n'appartient pas à un autre cube .
Sous ces conditions, \( K - \{\sigma, \tau\} \) est un complexe cubique et il est homotopiquement équivalent à \( K \) (il a la même topologie)
Par transitivité, deux complexes cubiques \( K, K' \) sont homotopiquement équivalent si on peut passer de l'un à l'autre avec des collapses élémentaires.
Un point d'un objet discret est simple si sa suppression ne change pas la topologie (des complexes cubiques).
Il suffit de connaître son voisinage ⇒ On peut utiliser la transformée en tout-ou-rien avec moins de 256 masques.
Exercice
Déterminer si le point est simple ou pas
Masques pour détecter les points simples (plus rotations) :
