Morphologie mathématique
Géométrie discrète - Master GIG
Opérateurs de base
Contexte
- Théorie inventée à Paris en 1964 par Georges Matheron et Jean Serra
- Approche non linéaire : pas de convolution (mais presque)
- Base théorique solide (treillis), bonnes propriétés
- Extension en nD évidente, extension en niveau de gris élégante (et utile)
Élément structurant : \(B \subset \mathbb{Z}^2\) "petit"
Autres interprétations : matrice ou image avec une origine.
Exemples :
- \( B = N_4(0,0) = \{ (0,0), (1,0), (-1,0), (0,1), (0-1) \} \)
- \( B = N_8(0,0) \)
- \( B = B_8(r) = \{ x \in \mathbb{Z}^2, \|x\|_{\infty} \leq r \} \)
- \( B = [-5, 5] \times [0] \)
Opérations sur un élément structurant :
- Translation par un point \(z = (z_1, z_2) \in \mathbb{Z}^2\) : \[ B_z = z + B = \{ z+b \vert b \in B\} \]
- Réflexion : \[ \hat{B} = - B = \{ - b \vert b \in B\} \] \( B \) est le plus souvent symétrique
Érosion
Opérations sur un objet discret \(A \subset \mathbb{Z}^2\) avec un élément structurant : \[ A \ominus B = \varepsilon_B(A) = \{ z \vert B_z \subset A \} \]
Propriétés de l'érosion :
- \( A \ominus B = \{ z \vert B_z \cap A^c = \emptyset \} \) : définition équivalente
- \( A \ominus B \subset A \) : l'objet rétrécit
- \( A \subset A' \Rightarrow \varepsilon_B(A) \subset \varepsilon_B(A') \) : croissante
Dilatation
Opération « contraire » (duale) : \[ A \oplus B = \delta_B(A) = \{ z \vert \hat{B}_z \cap A \neq \emptyset \} \]
Propriétés de la dilatation :
- \( A \oplus B = \cup \{ B_z \vert z \in A \} \) : définition équivalente
- \( A \subset A \oplus B \) : l'objet gonfle
- \( A \subset A' \Rightarrow \delta_B(A) \subset \delta_B(A') \) : croissante
Dualité érosion/dilatation
- \( (A \ominus B)^c = A^c \oplus \hat{B} \) : éroder un objet = dilater son complémentaire
- \( (A \oplus B)^c = A^c \ominus \hat{B} \) : dilater un objet = éroder son complémentaire
Plus d'opérateurs
Ouverture
Érosion, puis dilatation : \[ A \circ B = (A \ominus B) \oplus B \]
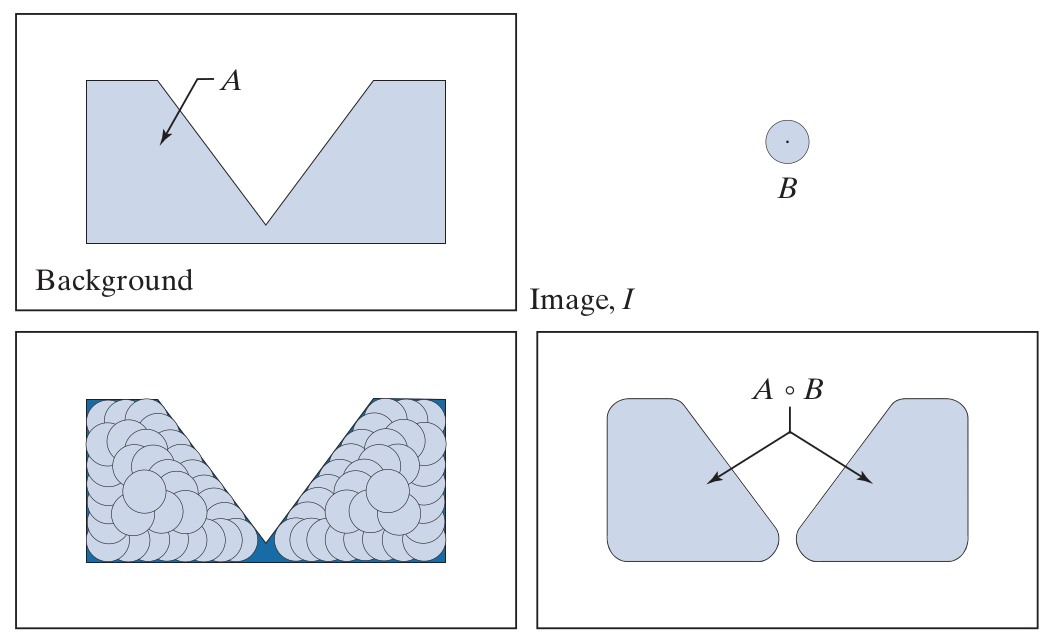
Propriétés de l'ouverture :
- \( A \circ B = \cup \{ B_z \vert B_z \subset A \} \) : définition équivalente
- \( A \circ B \subset A \)
- \( A \subset A' \Rightarrow (A \circ B) \subset (A' \circ B) \)
- \( (A \circ B) \circ B = A \circ B \) : idempotent
Exemple
Supprimer le bruit



Fermeture
Dilatation, puis érosion : \[ A \bullet B = (A \oplus B) \ominus B \]
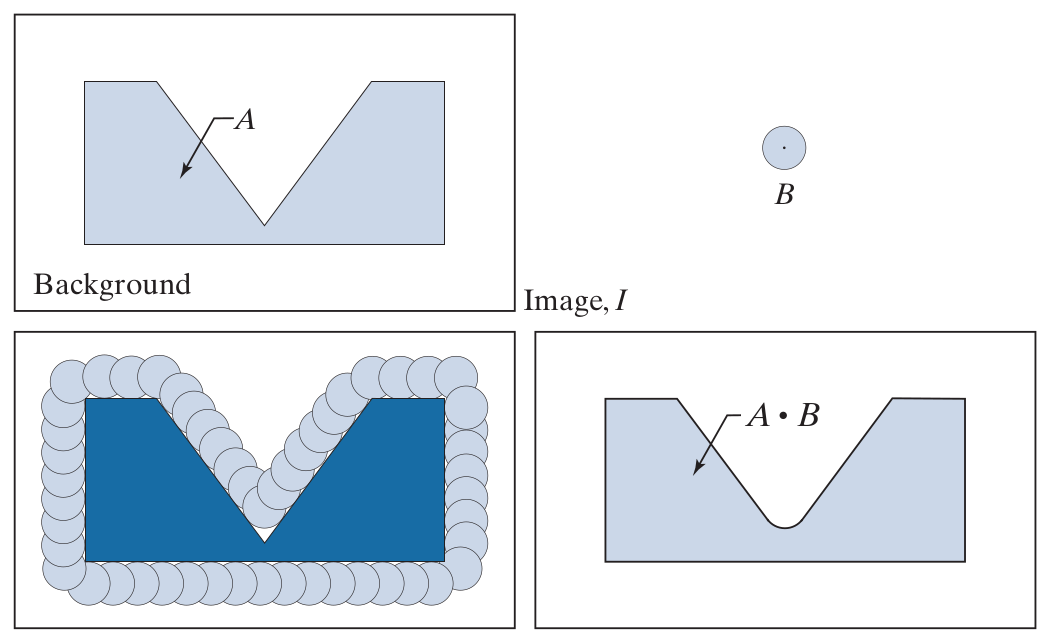
Propriétés de la fermeture :
- \( A \bullet B = \left( \cup \{ B_z \vert B_z \cap A = \emptyset \} \right)^c\) : définition équivalente
- \( A \subset A \bullet B \)
- \( A \subset A' \Rightarrow (A \bullet B) \subset (A' \bullet B) \)
- \( (A \bullet B) \bullet B = A \bullet B \) : idempotent
Exemple
Supprimer le bruit



Dualité :
- \( (A \bullet B)^c = (A^c \circ \hat{B}) \)
- \( (A \circ B)^c = (A^c \bullet \hat{B}) \)
Transformée en tout-ou-rien
Soit \( B = (C, D) \) une paire d'éléments disjoints, \[ A \odot B = (A \ominus C) \cap (A^c \ominus D) \]
Autre interprétation : matrice avec des 0, des 1 ou rien