Homologie persistante
SMACUD1L - Master IMD
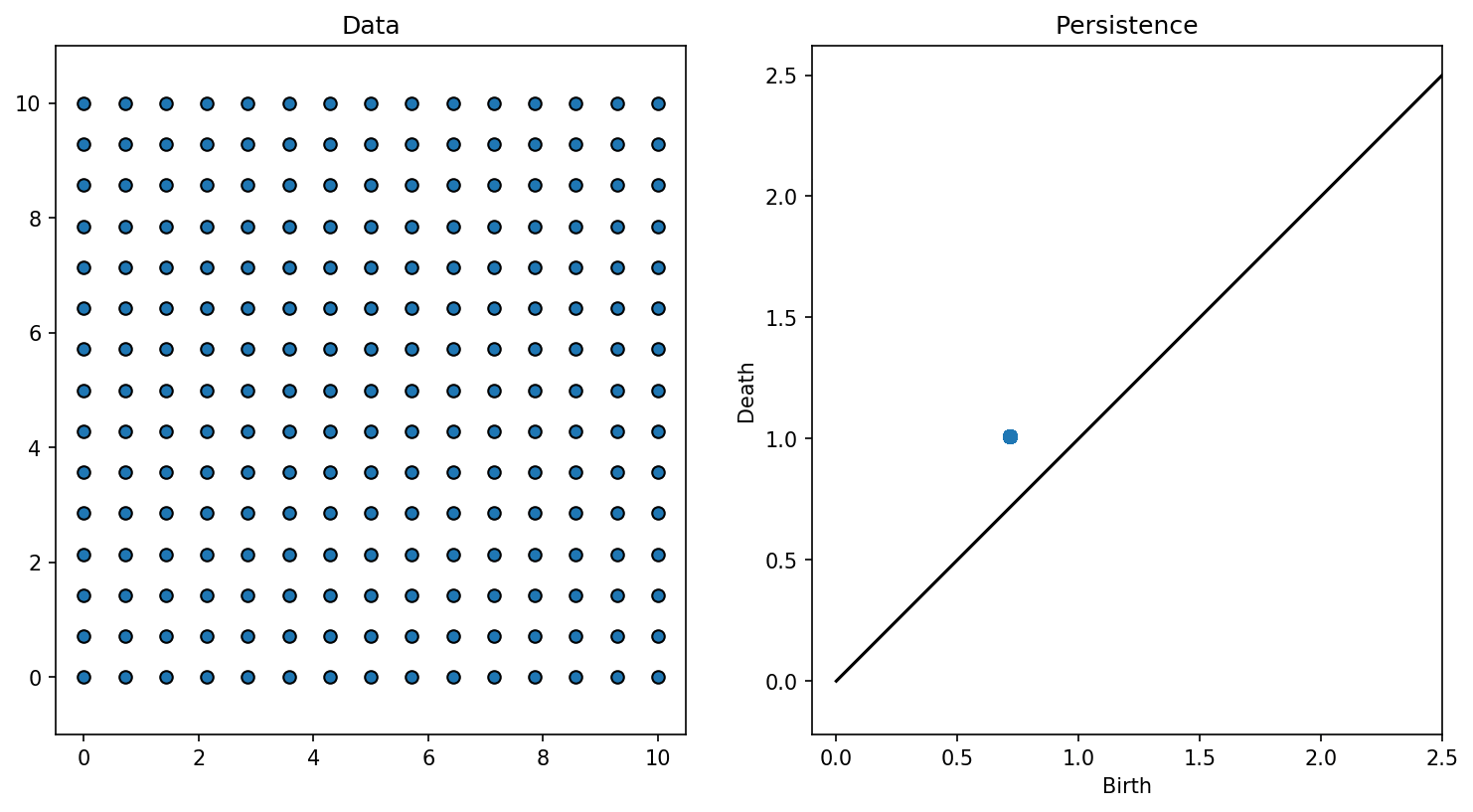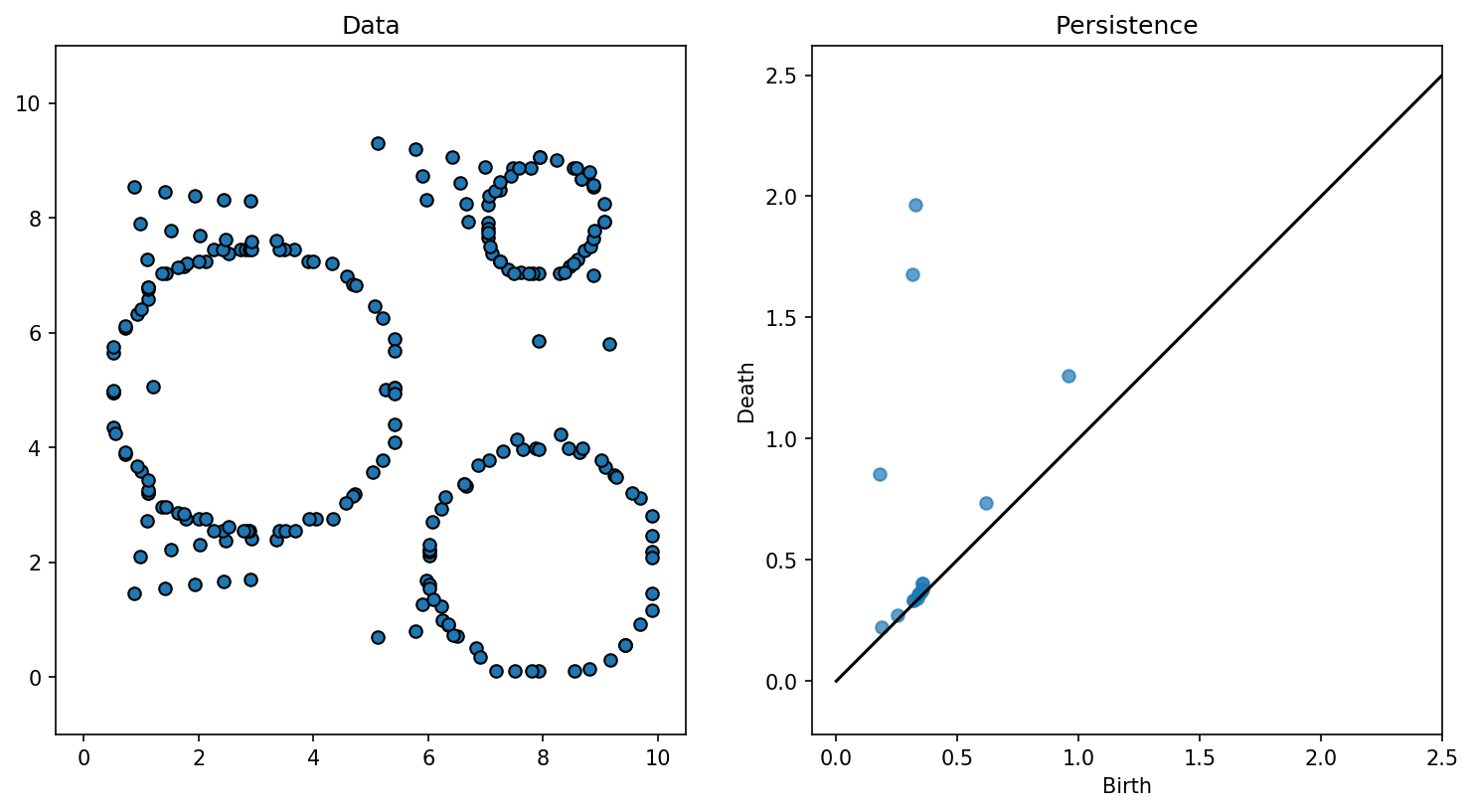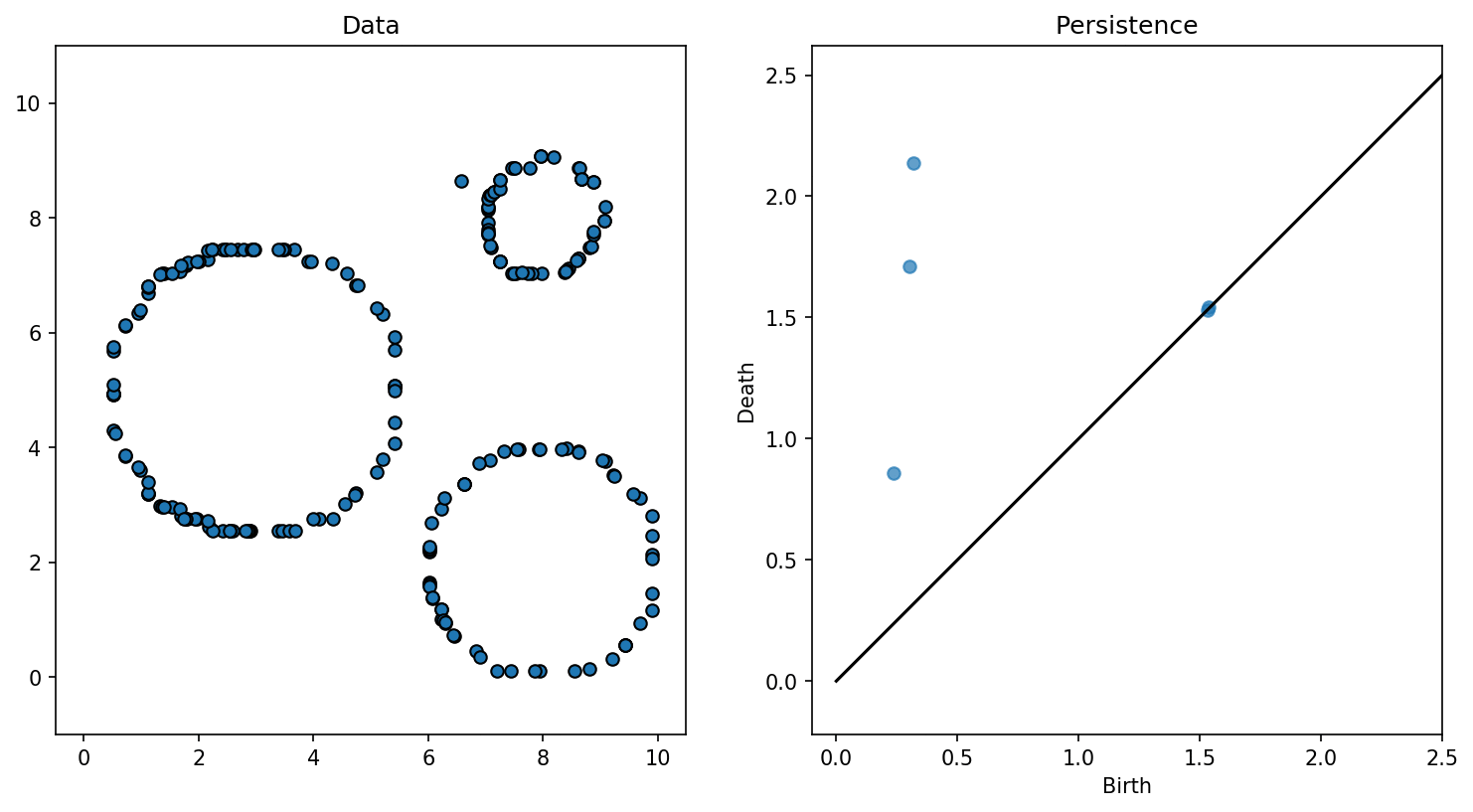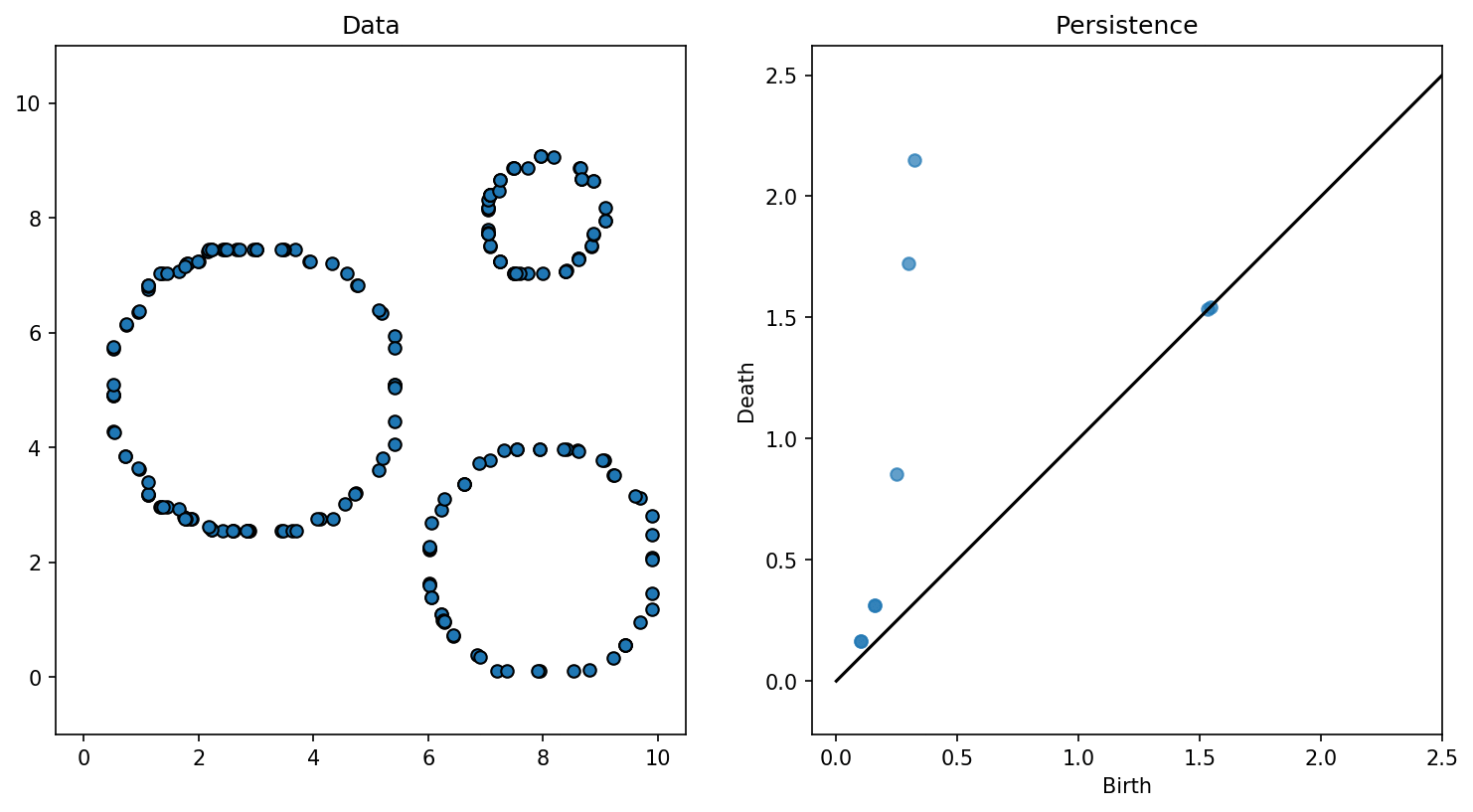
Observations :
- Le nombre de trous varie en fonction du paramètre
- Certains trous restent dans les étapes suivantes
- Si on bouge un peu les points, le comportement global est similaire
Rappel d'homologie
- \(K\) : complexe simplicial fini
- \(K_q\) : simplexes de \(K\) de dimension \(q\)
- \( (C, \partial) \) : complexe de chaînes induit par \(K\) avec anneau de coefficients = \(\mathbb{Z}/2\mathbb{Z} \) (corps)
- \(H_q = \ker(\partial_q) / \text{im}(\partial_{q+1}) \) : groupe d'homologie de dimension \(q\) de \(K\) (espace vectoriel)
- \(\beta_q = \dim(H_q)\) = nombre de Betti de dimension \(q\)
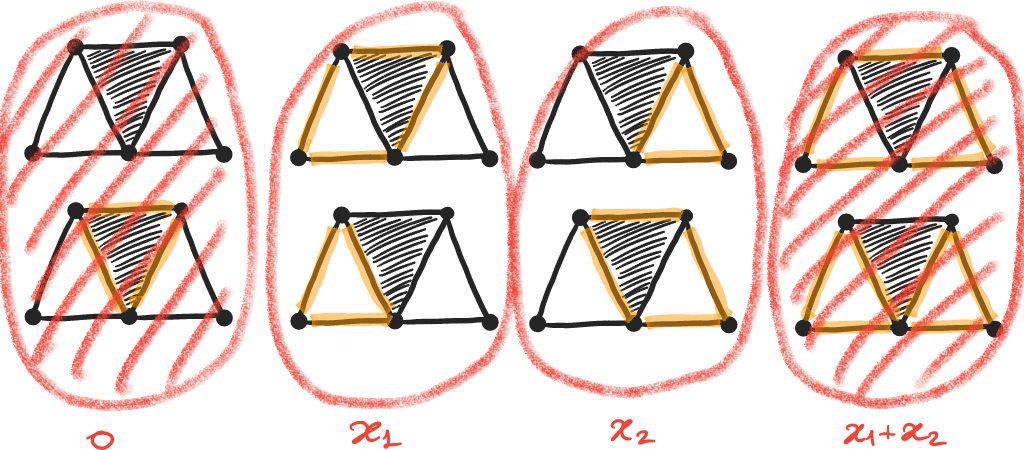
Exemple 1
Cycles, classes d'équivalence, base d'homologie :


Soient \(K \subset K'\). L'application inclusion \(inc : K \longrightarrow K'\) induit une application linéaire \[\iota : H_q(K) \longrightarrow H_q(K')\] entre ses groupes d'homologie (exercice)
Exemple 2
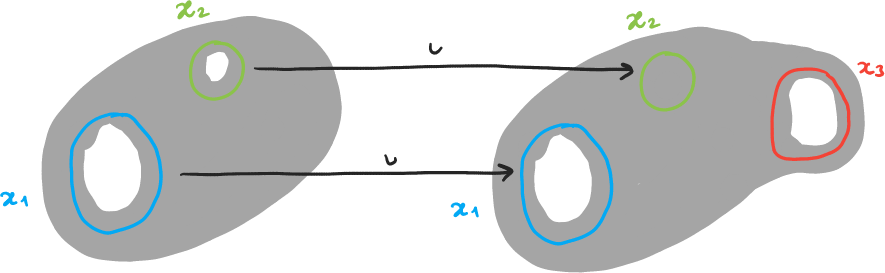
Même nombre de trous, mais
- \(\iota\) n'est pas injective ⇒ « un trou de K est bouché dans K' »
- \(\iota\) n'est pas surjective ⇒ « K' a un trou qui n'était pas dans K »
Morale
L'application \(\iota : H_q(K) \longrightarrow H_q(K')\) montre
la relation entre les trous de \(K \subset K'\)
Définir la persistance
Filtration : suite de complexes imbriqués \[K^1 \subset K^2 \subset \cdots \subset K^n\]

Exemple 3
Soit \(f: K \rightarrow \mathbb{R}\) telle que :
- \(\sigma \subset \tau \Rightarrow f(\sigma) \leq f(\tau)\)
- \( f(K) = \{a_1 < a_2 < \cdots < a_n\} \)
Alors \( f^{-1}(-\infty, a_1] \subset f^{-1}(-\infty, a_2] \subset \cdots \) est une filtration (exercice)
Exercice 1
Compléter cette fonction pour qu'elle définisse une filtration
Exemple 4
Soit \(f: K_0 \rightarrow \mathbb{R}\) quelconque. On définit \( \bar{f}: K \rightarrow \mathbb{R} \)
- \( \bar{f}(\sigma) = f(\sigma) \), si \( \sigma \in K_0 \)
- \( \bar{f}(\sigma) = \max\{f(\tau) \vert \tau \subset \sigma, \tau \in K_0\} \), sinon
Alors \( \bar{f} \) définit une filtration (exercice)
Exercice 2
Éteindre cette fonction aux simplexes de dimension supérieure
Exemple 5
Soit \(K^1 \subset \cdots \subset K^n\) une filtration. On définit \( f: K^n \rightarrow \mathbb{R} \), \( f(\sigma) = i \Leftrightarrow \sigma \in K^{i} \setminus K^{i-1} \)
Alors \( f \) définit la filtration donnée (exercice)
Donc, on peut travailler avec une filtration (suite de complexes) ou avec une fonction monotone : \( \sigma \subset \tau \Rightarrow f(\sigma) \leq f(\tau) \)
Soit \( f \) monotone, \( f(K) = \{ a_1 < \cdots < a_n\} \). Notation :
- \( K^i = f^{-1}\left( -\infty, a_i \right] \)
- \(\iota_q^{i,j}: H_q(K^i) \longrightarrow H_q(K^j)\) application linéaire induite par l'inclusion (\( 1 \leq i \leq j \leq n \))
- \( \beta_q^{i,j} = \dim( \text{im}(\iota_q^{i,j}) ) \) : nombres de Betti persistants
- \( \mu_q^{i,j} = \beta_q^{i,j-1} - \beta_q^{i-1,j-1} - \beta_q^{i,j} + \beta_q^{i-1,j} \) (\( 1 \leq i < j \leq n+1,\quad \beta_q^{0,j} = \beta_q^{i,n+1} = 0 \))
Exercice 3
- Quelle inégalité entre \( \beta_q(K^i) \) et \( \beta_q^{i,j} \) ?
- Quelle inégalité entre \( \beta_q(K^j) \) et \( \beta_q^{i,j} \) ?
En français
- \( \beta_q^{i,j-1} \) = nombre de trous de \( K^i \) qui sont encore dans \( K^{j-1} \)
- \( \beta_q^{i,j-1} - \beta_q^{i-1,j-1} \) = nombre de trous qui apparaissent dans \( K^i \) et sont encore dans \( K^{j-1} \)
- \( \beta_q^{i,j} - \beta_q^{i-1,j} \) = nombre de trous qui apparaissent dans \( K^i \) et sont encore dans \( K^{j} \)
- \( \mu_q^{i,j} \) = nombre de trous qui apparaissent dans \( K^i \) et disparaissent dans \( K^{j} \)
Le diagramme de persistance de dimension q de \( f \) est le multi-ensemble \( D_q(f) \subset \overline{\mathbb{R}}^2 \) avec
- les points \( (a_i, a_j) \) avec multiplicité \( \mu_q^{i,j} \) (\( a_{n+1} = \infty \))
- les points \( (x, x) \) avec multiplicité \( \infty \), pour tout \( x \in \mathbb{R} \)
Les \( (a_i, a_j) \) sont les paires de persistance
Exemple 6
Homologie persistante de dimension 0
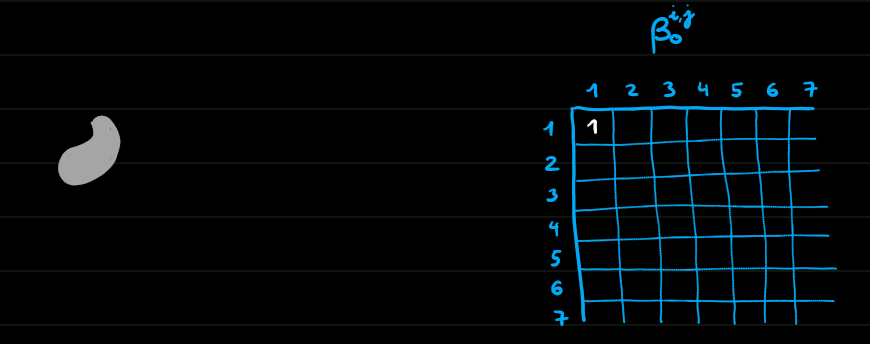
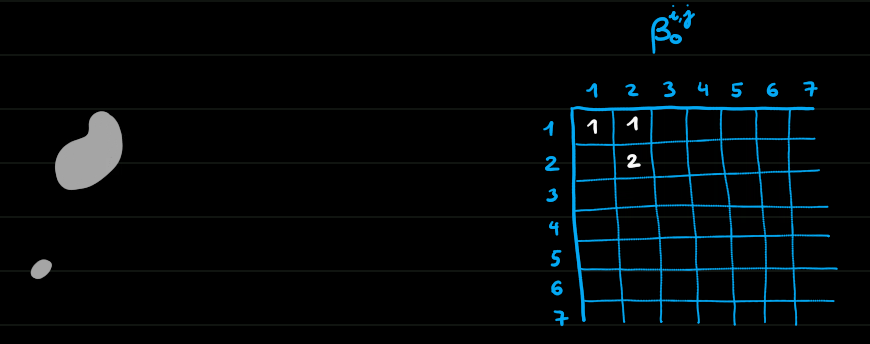
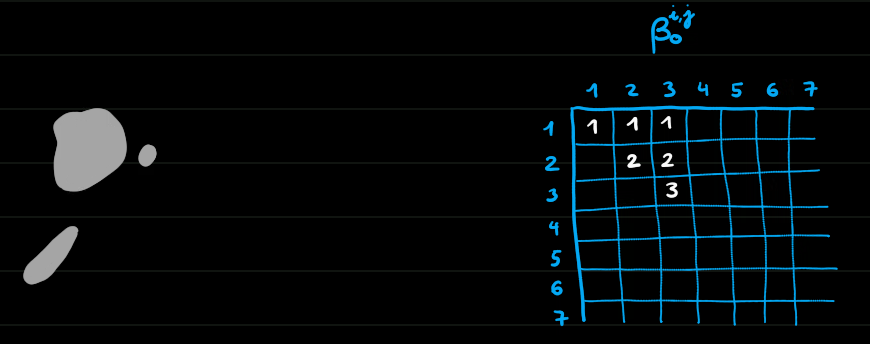
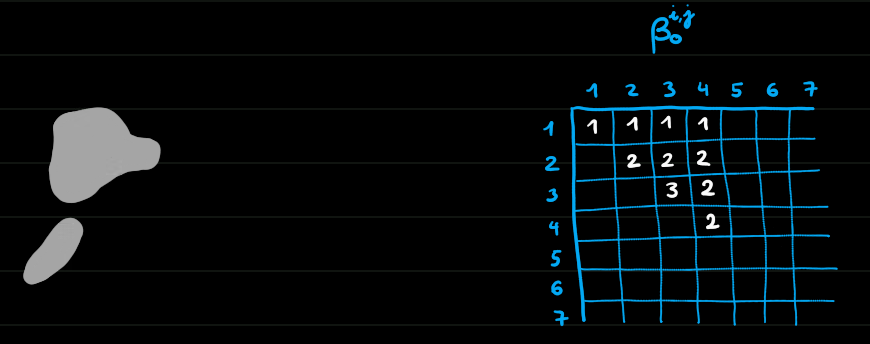
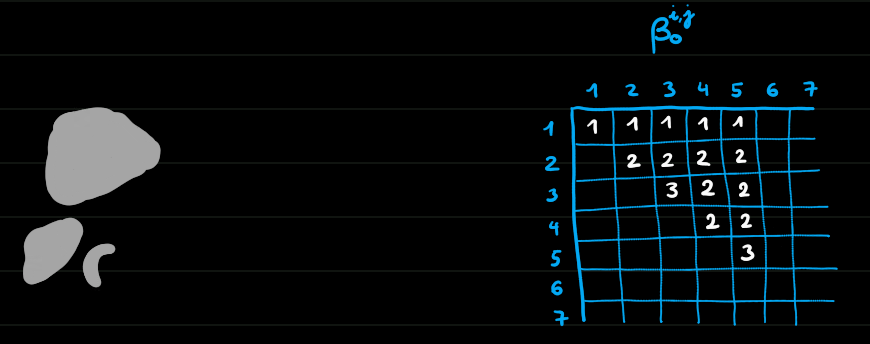
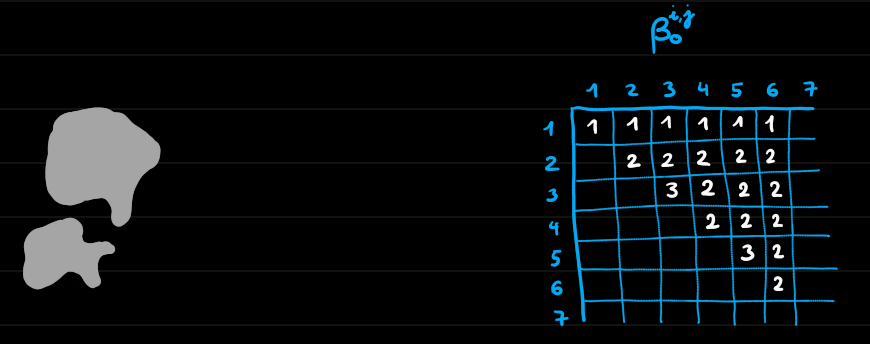
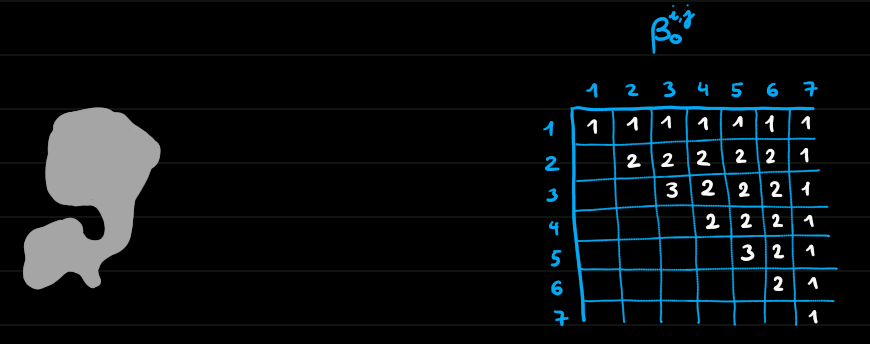

Morale
- On peut suivre les trous d'un complexe à un autre dans une filtration (ils ne sont pas indépendants)
- L'homologie persistante permet de définir la date de naissance et de mort d'un trou, donc aussi sa durée
Stabilité
Soient \( f, g: K \longrightarrow \mathbb{R} \). Leur distance est \[ \|f-g\|_{\infty} = \max_{\sigma \in K} |f(\sigma) - g(\sigma)| \]
Question : si \( f \) et \( g \) sont similaires, que se passe-t-il avec leurs diagrammes de persistance ? Comment les comparer ?
Distance de Hausdorff
Soient \( X, Y \) deux multi-ensembles de points de \( \mathbb{R}^2 \), \[ \begin{align*} d_H(X,Y) = \max \{ &\max_{x \in X} \min_{y \in Y} \|x-y\|_{\infty},\\ &\max_{y \in Y} \min_{x \in X} \|x-y\|_{\infty} \} \end{align*} \]
- Prends un \( x \in X \), regarde sa distance vers \( Y \)
- Fais la même chose pour chaque \( x \in X \) et prends la plus grande distance
- Échange \( X \) et \( Y \), prends encore la plus grande
Exercice 4
Distance de Hausdorff ?

Premier théorème de stabilité Cohen-Steiner et al, 2007
\[ d_H(D_q(f), D_q(g)) \leq \|f-g\|_{\infty} \]
En français : si on change un peu la fonction d'une filtration, son diagramme de persistance aura ses points à proximité
Exemple 7
Fonction \( f \) continue définie sur \( K \) un intervalle
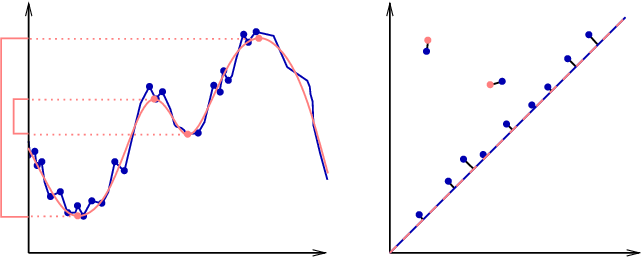
Une idée de pourquoi :
- Soit \( \delta = \|f-g\|_{\infty} \)
- \( f^{-1}(-\infty, x] \subset g^{-1}(-\infty, x + \delta] \)
- \( g^{-1}(-\infty, x] \subset f^{-1}(-\infty, x + \delta] \)
- On se sert de ces inclusions pour démontrer le théorème...
Distance bottleneck
\[ d_B(X,Y) = \min_{\gamma} \max_{x \in X} \|x - \gamma(x)\|_{\infty}, \] où \( \gamma:X \rightarrow Y \) bijective
- Fais un couplage entre les points de \( X \) et \( Y \), prends la plus grande distance entre les couples
- Parmi tous les couplages, prends la valeur la plus petite
Exercice 5
Distance bottleneck ?
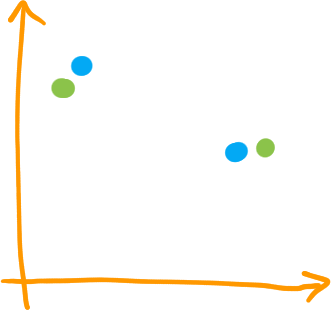
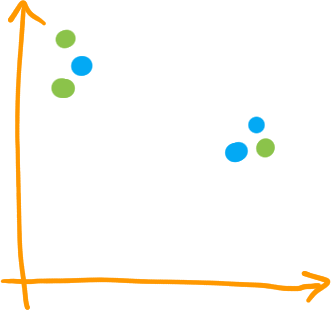
Deuxième théorème de stabilité Cohen-Steiner et al, 2007
\[ d_B(D_q(f), D_q(g)) \leq \|f-g\|_{\infty} \]
En français : si on change un peu la fonction d'une filtration, chaque point va bouger d'un peu
Comme \( d_H(X,Y) \leq d_B(X,Y) \), ce deuxième théorème est plus fort
Morale
Les théorèmes de stabilité nous disent que :
- Si la fonction contient des erreurs (estimation), les diagrammes restent pareils
- Les points près de la diagonale ( = trous avec une courte durée) ne sont pas importants (car indistinguables d'une erreur)
- Deux diagrammes différents ⇒ deux fonctions différentes, mais pas le contraire
Exercice 6
Deux fonctions très différentes avec des diagrammes identiques ?

Calcul (homologie standard)
- Complexe simplicial \(K\) ≃ liste de tuples
-
liste de tuples ≃ matrices de bord,
\( \partial_{q+1}(\langle v_1, \cdots, v_q \rangle) = \sum_{i=1}^q (-1)^{i+1} \cdot \langle v_1, \cdots, \hat{v}_i, \cdots, v_q \rangle \) - \( H_q(K) = \ker(\partial_q) / \text{im}(\partial_{q+1}) = (\mathbb{Z}/2 \mathbb{Z})^{\beta_q} \)
- \( \beta_q = \dim(\ker(\partial_q)) - \dim(\text{im}(\partial_{q+1})) \)
- \( \dim(\ker(\partial_q)) \), \( \dim(\text{im}(\partial_{q+1})) \) ? ⟶ Diagonalisation
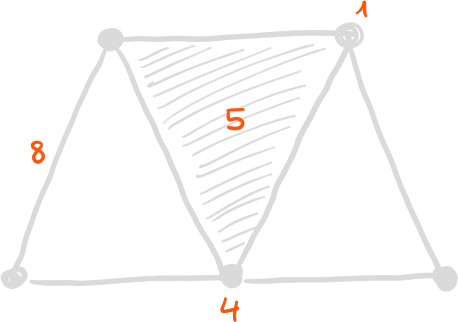
Exemple 8
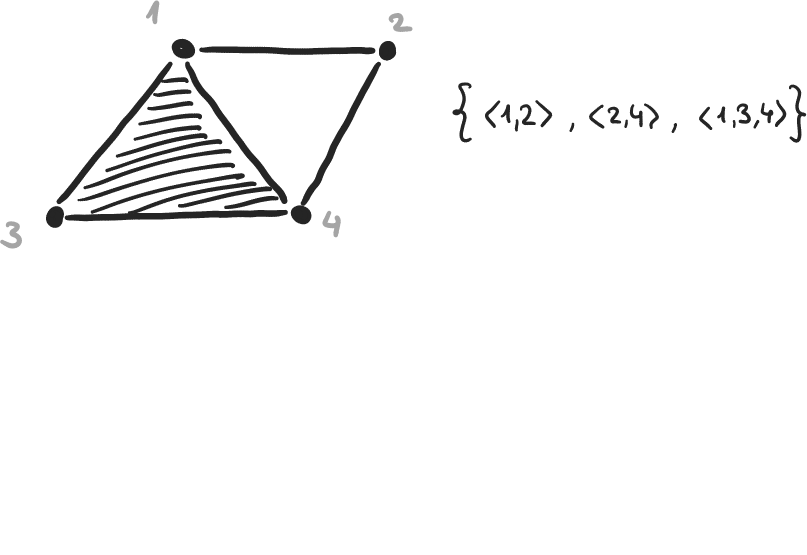
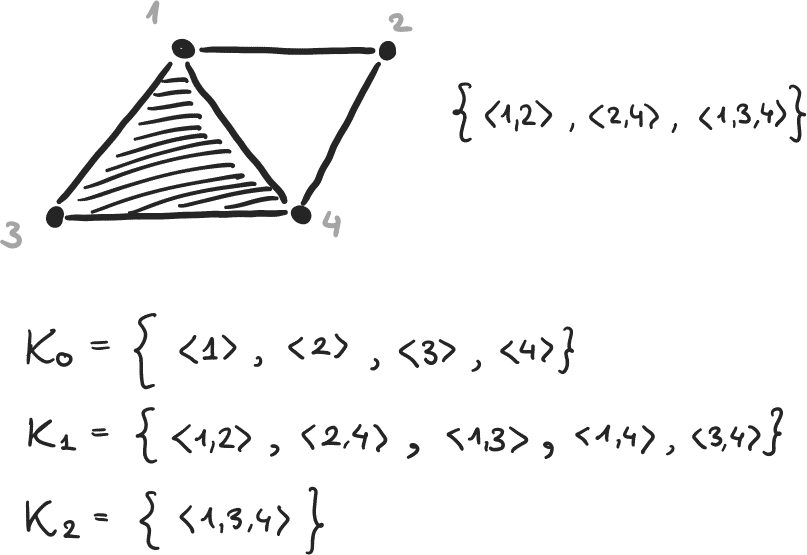
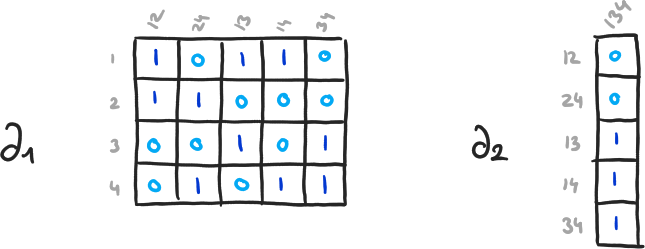
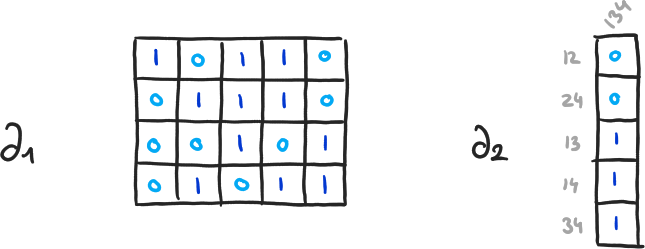
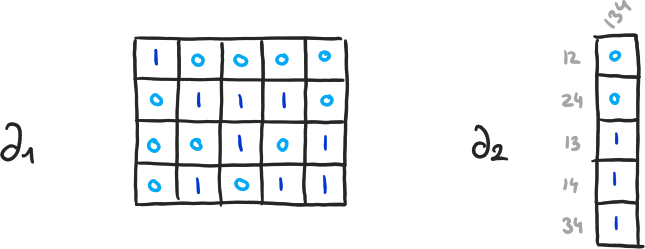
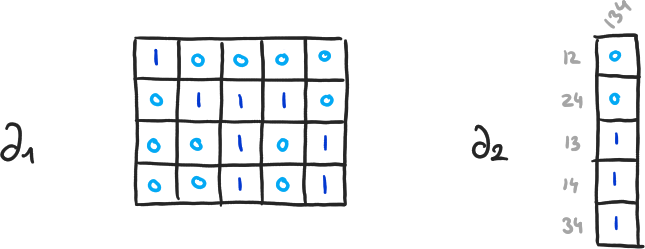
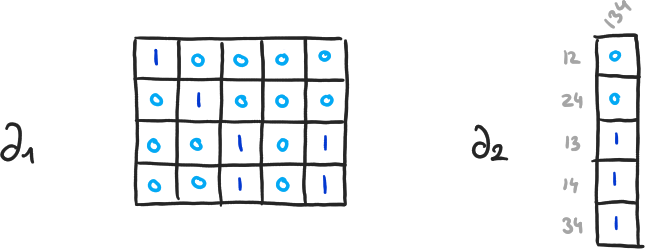
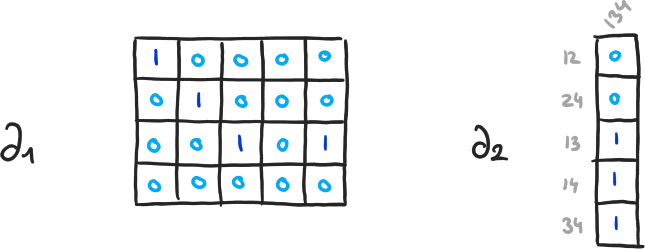
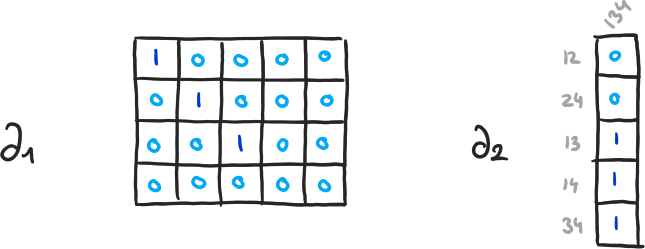
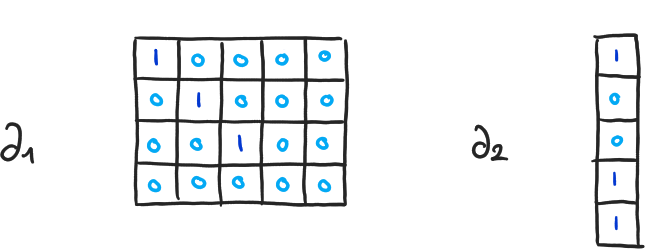
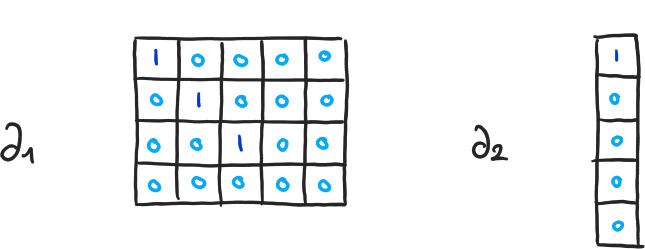
\( \beta_0 = 4-3, \beta_1 = 2-1, \beta_2 = 0-0 \)
Pour calculer les groupes d'homologie avec coefficients dans une anneau ( \( \mathbb{Z} \) ), il faut calculer la forme normale de Smith des matrices de bord

\( H_q = \mathbb{Z}^{4-3} \oplus \mathbb{Z}/2\mathbb{Z} \oplus \mathbb{Z}/6\mathbb{Z} \)
Calcul (homologie persistante)
Algorithme incrémental pour l'homologie
Algorithme pour calculer les nombres de Betti d'un complexe simplicial Delfinado et Edelsbrunner, 1992
Il faut trier les simplexes de façon à avoir une filtration :
- \(K = \{\sigma^1, \ldots, \sigma^n\}\)
- Pour tout j, \(K^j = \{\sigma^1, \ldots, \sigma^j\}\) est un complexe simplicial
β0, β1, β2 ← 0
for j = 1...n
q ← dim(σj)
if σj appartient à un cycle de Kj
βq ← βq + 1
else
βq-1 ← βq-1 - 1
return (β0, β1, β2)Idée de la preuve :
- Ajouter un q-simplexe incrémente \(\beta_q\) ou décrémente \(\beta_{q-1}\) (Théorème d'Euler-Poincaré)
- Si \(\sigma^j\) appartient à un cycle de \(K^j\) alors il y a un nouveau cycle par rapport à \(K^{j-1}\), et ce n'est pas un bord.
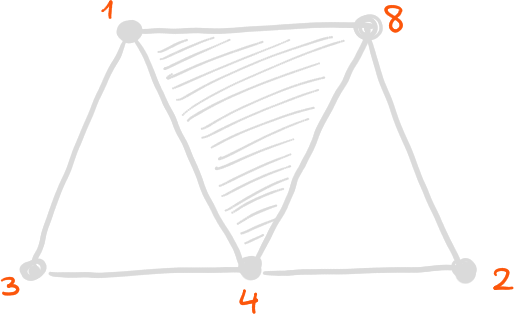
Exercice 7
Calculer les nombres de Betti

Deux types de simplexes :
-
Positif
: il appartient à un cycle dans \(K^j\)
⇒ « il ajoute un trou » -
Négatif
: il n'appartient pas à un cycle dans \(K^j\)
⇒ son bord est un cycle non trivial dans \(K^{j-1}\) (exercice)
⇒ « il supprime un trou »
Algorithme
L'algorithme incrémental peut être adapté pour calculer les paires de persistance. Il nous faudra :
- Bon choix des bases d'homologie
- Coupler les simplexes négatifs (un trou disparaît) avec des simplexes positifs (un trou apparaît)
Pour simplifier, on considère des filtrations avec un seul simplexe entrant à la fois.
Quand on arrive à un simplexe positif \( \sigma^i \) :
- nouveau cycle : \( g^i = \sigma^i + \sum_{l \in L} \sigma^l \)
- notons que pour tout \( l \in L, l < i \)
- on peut se restreindre à des \(\sigma^l\) négatifs (exercice)
- base de \( H(K^i) \) = base de \( H(K^{i-1}) \cup \{ g^i \}\)*
- Correspondance élément d'une base ↔ simplexe positif ↔ \( i \in [1, n] \)
Quand on arrive à un simplexe négatif \( \sigma^j \) :
- \( \partial(\sigma^j) \) cycle non trivial dans \( K^{j-1} \)
- \( \partial(\sigma^j) = \sum_{i \in I} g^i \) dans \( H(K^{j-1}) \)
- \( \sum_{i \in I} g^i \sim 0 \) dans \( H(K^{j}) \) ⇒ ils ne sont pas linéairement indépendants
- base de \( H(K^j) \) = base de \( H(K^{j-1}) \setminus \{ g^k \}, k \in I \) (lequel ?)
- Correspondance simplexe négatif ↔ ensemble de simplexes positifs précédents ↔ \( I \subset [ 1, j-1 ] \)
Pseudocode :
L0, L1, L2 ← ∅ // listes des paires
B0, B1, B2 ← ∅ // bases d'homologie
for j = 1...n
q ← dim(σj)
if σj est positif
Bq ← Bq ∪ {j}
else
I ← ∂(σj)
i ← max(I) // c'est lui, le plus jeune !
Bq-1 ← Bq-1 - {i}
Lq-1 ← Lq-1 ∪ {(i,j)}
foreach σi non couplé
q ← dim(σi)
Lq ← Lq ∪ {(i,n+1)}
return (L0, L1, L2)\( D_q = \{ (a_i, a_j) \vert (i,j) \in L_q \} \)
Exercice 8
Calculer les paires de persistance \( (i, j) \)

k-Triangle Lemma
Soit \( Q^{i,j} = ]-\infty, i] \times ]j, \infty[ \), alors
\( \beta_q^{i,j} = \#(D_q(f) \cap Q^{a_i, a_j}) \)
(exercice)
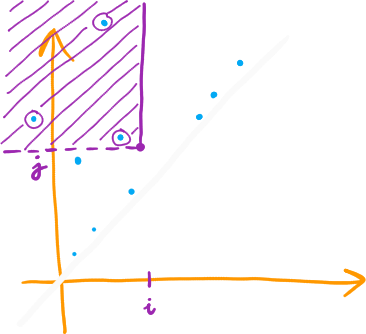
C'est la clé de la preuve de l'algorithme, on va démontrer que \( \beta_q^{i,j} = \#(L_q \cap Q^{i,j}) \)
Preuve de l'algorithme
On fixe \( q \) et \( i \), et on le démontre par induction sur \( k = j-i \geq 0 \).
Cas de base : Si \( i = j \) alors \( \beta_q^{i,i} = \beta_q(K^i) \).
D'autre part, \( \#(L_q \cap Q^{i,i}) \) =
- = nombre de paires \( (a,b) \in L_q, a \leq i < b\)
- = nombre \( q \)-simplexes positifs moins nombre \( (q+1) \)-simplexes négatifs à l'étape \( i \)
- = \( \beta_q(K^i) \) (comme l'algorithme incrémental)
Induction : Vrai pour \( \beta_q^{i,j} \). Deux possibilités pour \( \beta_q^{i,j+1} \) :
\( \beta_q^{i,j+1} = \beta_q^{i,j} \) ou \( \beta_q^{i,j+1} = \beta_q^{i,j} -1 \)
Si \( \sigma^{j+1} \) est un \(q\)-simplexe positif :
- \( \beta_q^{i,j+1} = \beta_q^{i,j} \)
- il y une paire \( (j+1, b) \in L_q, b > j+1 \)
- \( (j+1, b) \notin Q^{i,j} \Rightarrow \#(L_q \cap Q^{i,j+1}) = \#(L_q \cap Q^{i,j}) \)
- \( \beta_q^{i,j+1} = \#(L_q \cap Q^{i,j+1}) \)
Si \( \sigma^{j+1} \) est un \( (q+1) \)-simplexe négatif :
- \( \partial(\sigma^{j+1}) = \sum_{i \in I} g^i \)
- \( \beta_q^{i,j+1} = \beta_q^{i,j} -1 \Leftrightarrow \max(I) \leq i \) (exercice)
- \( \max(I) \leq i \Leftrightarrow \#(L_q \cap Q^{i,j+1}) = \#(L_q \cap Q^{i,j}) - 1\)
- \( \beta_q^{i,j+1} = \#(L_q \cap Q^{i,j+1}) \) □
Ce qui reste :
- Filtration générale, avec plusieurs simplexes entrant en même temps.
- L'algorithme explicite pour savoir si un simplexe est positif, négatif, et son bord dans la base de \( H_q^{j} \)
Algorithme explicite
Il suffit une élimination gaussienne en \( \mathcal{O}(n^3) \)
Notation : \(D\) matrice de bord, toutes dimension confondues
\( D = (d_{ij}) \) telle que \( \partial(\sigma_j) = \Sigma_i \left( d_{ij} \cdot \sigma_i \right) \)
for j = 1...n
if Cj ≠ 0
i ← max(k; dkj = 1)
// élimination gaussienne avec le pivot dij
for k = 1...n
Rk ← Rk + dkj Ri
for k = 1...n
Ck ← Ck + dik Cj- \( M = \{ (\sigma_i, \sigma_j) \vert d_{ij} = 1 \} \) (simplexes couplés)
- \( U = K - M \) (simplexes non couplés)
- \( D_q(f) = \{ (f(\sigma_i), f(\sigma_j)) \vert (\sigma_i, \sigma_j) \in M, \dim(\sigma_i) = q \} \cup \{ (f(\sigma_k), \infty) \vert \sigma_k \in U, \dim(\sigma_k) = q \} \)
Exemple 9
Calculer les paires de persistance \( (i, j) \)


Morale
- Algorithme aussi basé sur la Forme Normale de Smith
- C'est toujours le plus jeune trou qui meurt
Applications
Quelques applications :
- Traitement d'images : reconstruction de contours
- Robotique : comment attraper un objet
- Visualisation scientifique : distinguer les parties importantes
- Analyse de formes : mesurer les trous
1. Traitement d'images

Comment reconnaître les contours ?

-
Entrée : ensemble fini de points \( P \subset \mathbb{R}^2 \)
Il devrait ressembler à un échantillon sur un graphe planaire - Sortie : un graphe planaire \( G \)
Si l'ensemble de points représente assez bien la forme, on devrait la retrouver
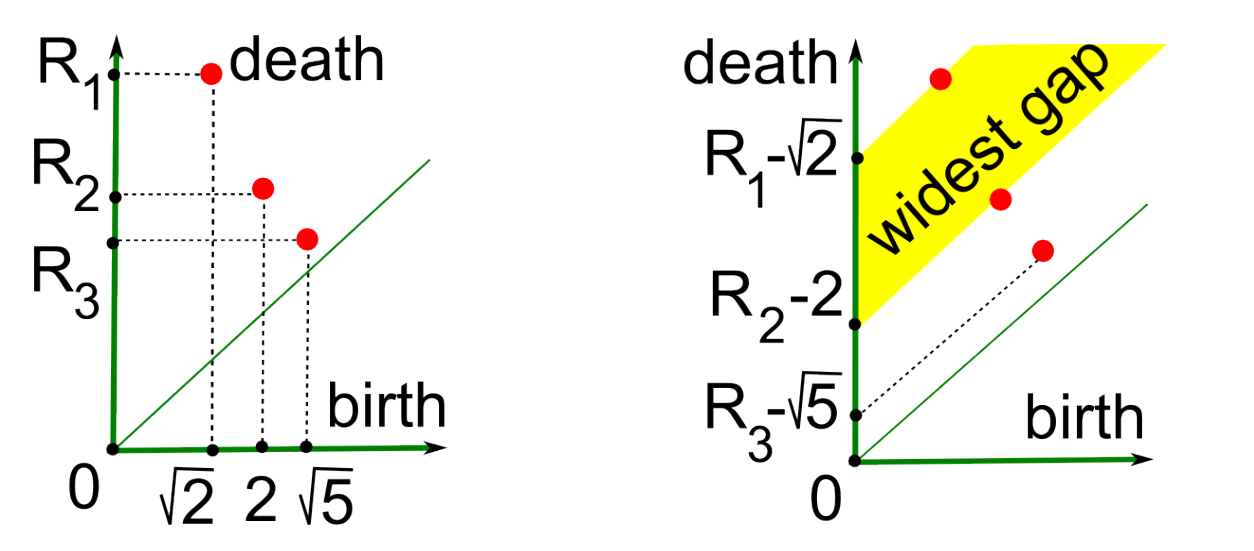
Algorithme :
- Construis une filtration avec des boules croissantes centrées sur les points (α-complexe)
- Calcule le diagramme de persistance de dimension 1 (composantes connexes ⇒ très rapide)
- Ignore les paires les plus proches de la diagonale à partir d'un seuil (widest gap) ⟵ clé de l'algorithme
- Le graphe \( G \) est formée par les cycles d'homologie des paires qui restent
Alpha complexe : filtration sur un ensemble de points \( P \subset R^2 \)
- Complexe : triangulation de Delaunay d'un ensemble de points
-
Fonction de filtration \( f \) :
- sur les 2-simplexes : rayon du cercle circonscrit du triangle
- sur les 1-simplexes : rayon du cercle circonscrit de l'arête (s'il ne contient pas d'autre point), minimum des valeurs des cofaces sinon
- sur les 0-simplexes : 0
- Propriété : \( f^{-1}(-\infty, a] \cong \) union des boules de rayon \( a \) centrées sur les points de \( P \)
Exemple 10
Exercice 9
Quelle est la sortie de l'algorithme pour ces données ?

2. Robotique

Question : comment attraper un objet à l'aide d'une main robotique et de la gravité ?
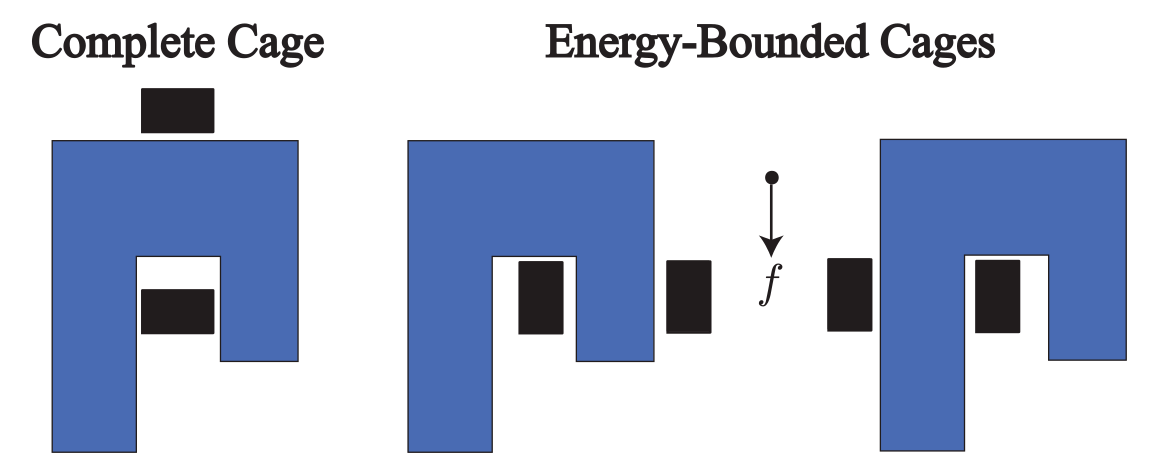
Observation : il y a plusieurs façons de l'attraper ; certaines sont meilleurs qu'autres
Filtration : espace de translations invalides + un rideau qui descend
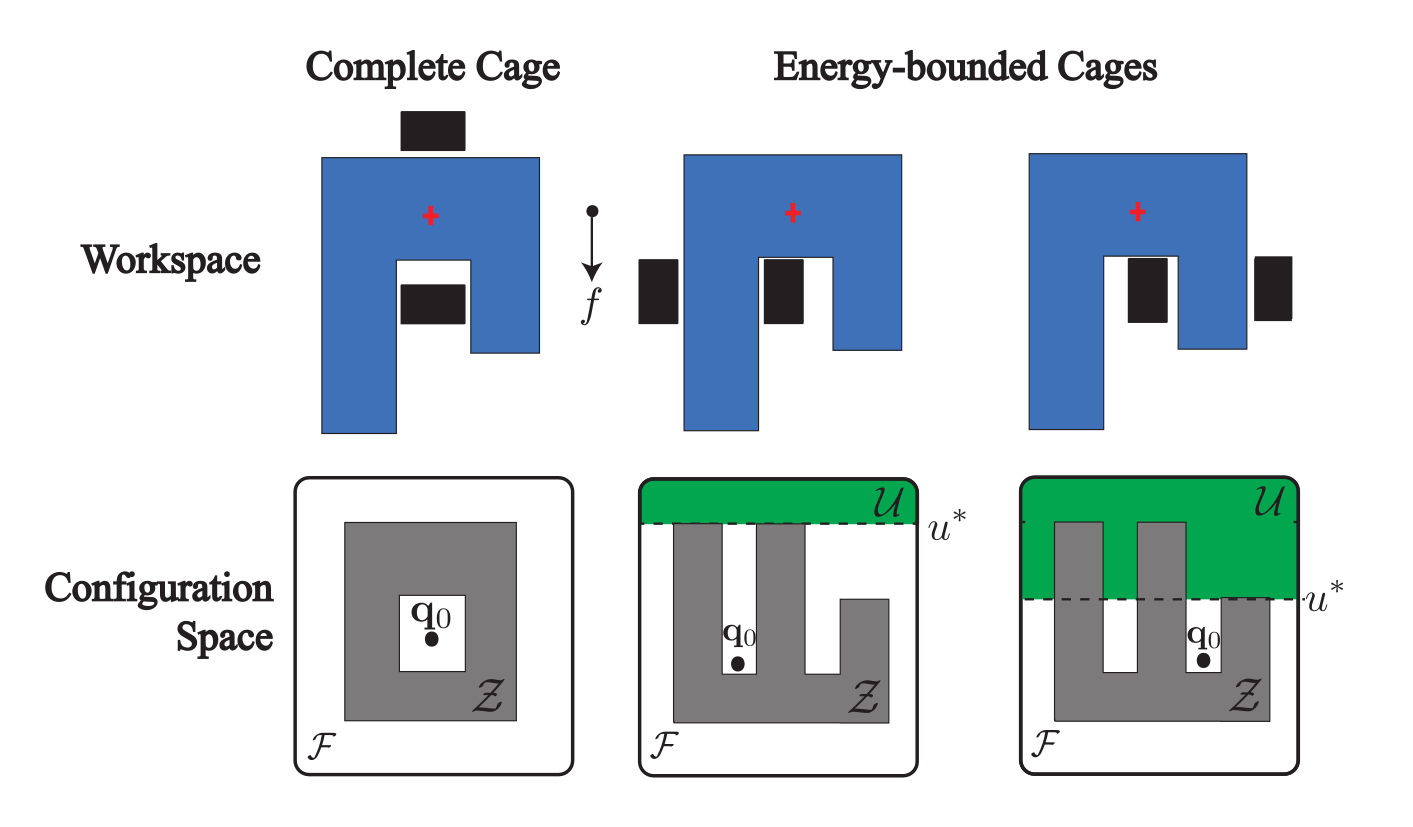
\( (x,y) \in D_1 \) ⇒ il y a une façon d'attraper l'objet et la quantité d’énergie nécessaire pour s'échapper est \( y - x \)
En pratique :
- Translations et rotations ⇒ espace de configurations sans collision \( F \subset \mathbb{R}^2 \times \mathbb{S}^1 \)
- Complexe : échantillon sur les configurations invalides et triangulation de Delaunay
- Filtration définie sur les arêtes : \( -\infty \) si longueur sous un seuil, \( \min(-y) \) sinon. On regarde \( D_2 \)
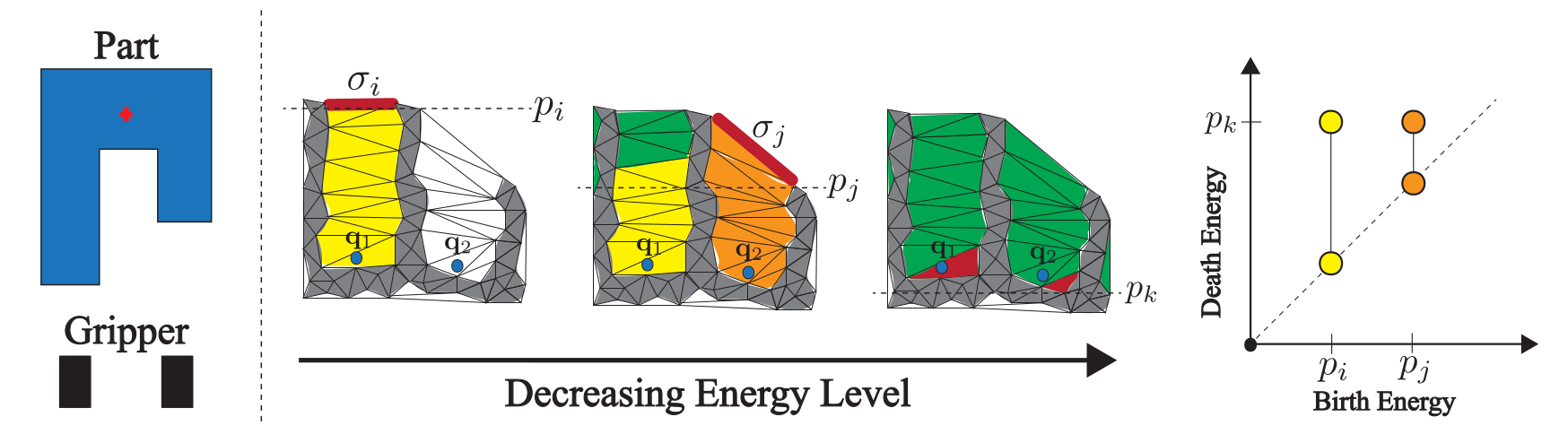
Exemple 11
3. Visualisation scientifique


Problème : visualiser la formation de doigts dans un écoulement d'eau salée
Données :
- Pour chaque pas de temps \( k \), un ensemble fini \( P_k \subset \mathbb{R}^4 \)
- Un élément \( (x, y, z, c) \) correspond à un point avec coordonnées spatiales \( (x, y, z) \) avec concentration de sel \( c \)
Étapes :
- Interpoler la concentration sur l'espace
- Séparer l'eau salée de l'eau non-salée (seuillage)
- Détecter les différents doigts (segmentation)
- Relier les différents doigts entre les pas de temps
Détails de l'étape 3 (segmentation) :
- Fonction de filtration : distance géodésique (négative) vers la base
- Seuillage du diagramme de persistance de dimension 0 proportionnel à l'image de la fonction (10%)
- Chaque sommet est associé avec le maximum le plus proche


Exemple 12
4. Analyse de formes


Question : comment distinguer les trous d'un objet ?
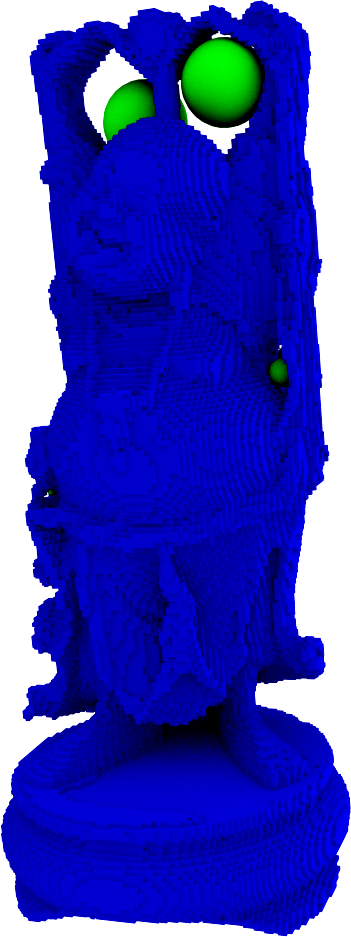
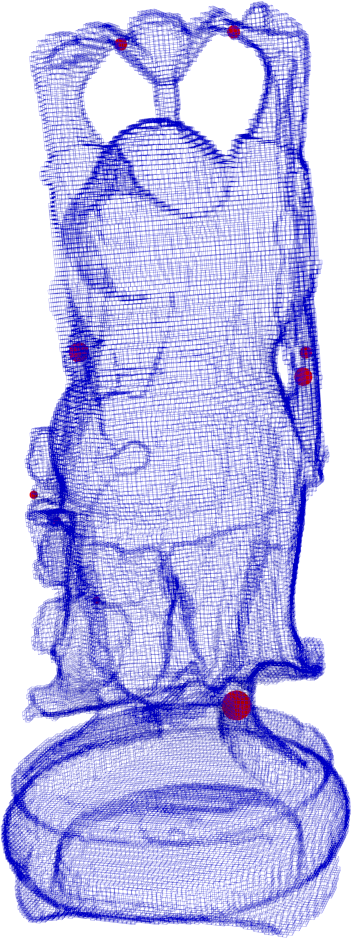
Érosions + dilatations = filtration
- \( D_q \cap Q^{0,0} \) = \( \beta_q \) paires \( (- a_i, b_i) \) avec \( a_i, b_i \geq 0 \)
- Une paire \( (a_i, b_i) \) pour chaque trou
-
\( a_i \) : de combien il faut éroder l'objet pour casser ce trou
= épaisseur -
\( b_i \) : de combien il faut dilater l'objet pour remplir ce trou
= largeur
De plus, le couplage de l'algorithme de l'homologie persistante permet de définir les deux centres de chaque trou


Stabilité : la distance entre les paires de deux objets \( X \) et \( Y \) est bornée par \[ d_H(X, Y) + d_H(X^c, Y^c) \]
En français : si on perturbe la frontière de l'objet, l'épaisseur et la largeur de chaque trou reste à peu près la même
Morale
- La stabilité des diagrammes permet de dégager le bruit
- En même temps, on peut distinguer les features les plus importantes (potentiellement)
- On utilise souvent l'homologie persistante en dimension 0 (calcul beaucoup plus rapide)
Conclusion
- Homologie persistante = extension de l'homologie à une suite de complexes
- Stabilité ⇒ correction, classement, comparaison
- Complexité worst-case cubique, mais presque linéaire en pratique
- Très à la mode car elle permet de faire de petites erreurs
Quelques ressources :